Recursion

Class Material

• Slides can be found here.

---

Geometry Series Formulae

---

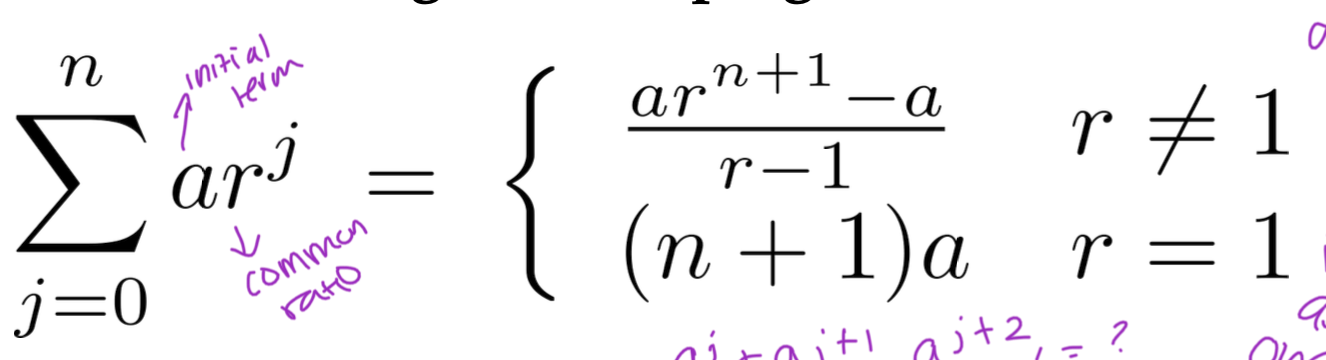
Solving Recurrences

1. Logarithm Rules and Geometric Series

Check slides: example with $O(n^{\log_2{3}})$ becoming $O(n^{n^{1.59}})$

2. Guessing and Substitution, then prove by induction

$T(n) = T(n-1) + n$

We guess that: $T(n) \leq cn^2$ (this is our induction hypothesis)

$$\begin{aligned} T(n) &\leq cn^2 \\ T(n-1) &\leq c(n-1)^2 \end{aligned}$$

We assume that $T(n) \leq cn^2$ is true, and we have to prove that $T(n-1) \leq c(n-1)^2$ still works.

$$\begin{aligned} T(n-1) &\leq c(n-2)^2+n-1 \\ &\leq cn^2-4nc+4c+n-1 \\ &\leq cn^2-4c(n-1)+n-1 \end{aligned}$$

As long as $c<\frac{1}{4}$ and $n>1$, $cn^2-4c(n-1)+n-1$ will be less than $cn^2$.

Hint: Solve $-4c(n-1)+n-1>0$

See that:

$$\begin{aligned} cn^2-4c(n-1)+n-1 &\leq cn^2 \\ \end{aligned}$$

Which means that $T(n-1) \leq c(n-1)^2$ is true.

$\therefore$ By induction, $T(n) \leq cn^2$ is true.

Pro-tip

In a recurrence of this form:

$$T(n) = a \cdot T(z \cdot \frac{n}{b}) + f(n)$$

As long as $\frac{z}{b} < 1$, the recursion will converge (problem size decreasing).

For example:

• $T(n) = T(\frac{5n}{2}) + n$ will diverge. This is $O(\infty)$.
• $T(n) = 5T(\frac{2n}{3}) + n^2$ will converge. We can solve this recurrence with the Master Theorem.

3. Master Theorem

Check slides: Master Theorem v1 for Big-Oh and v2 for Big-Theta

• Use intuition to understand the 3 cases of Master Theorem...
• Which part of the recursion dominates, and why? (leaves dominates, vs work per level dominates, etc)

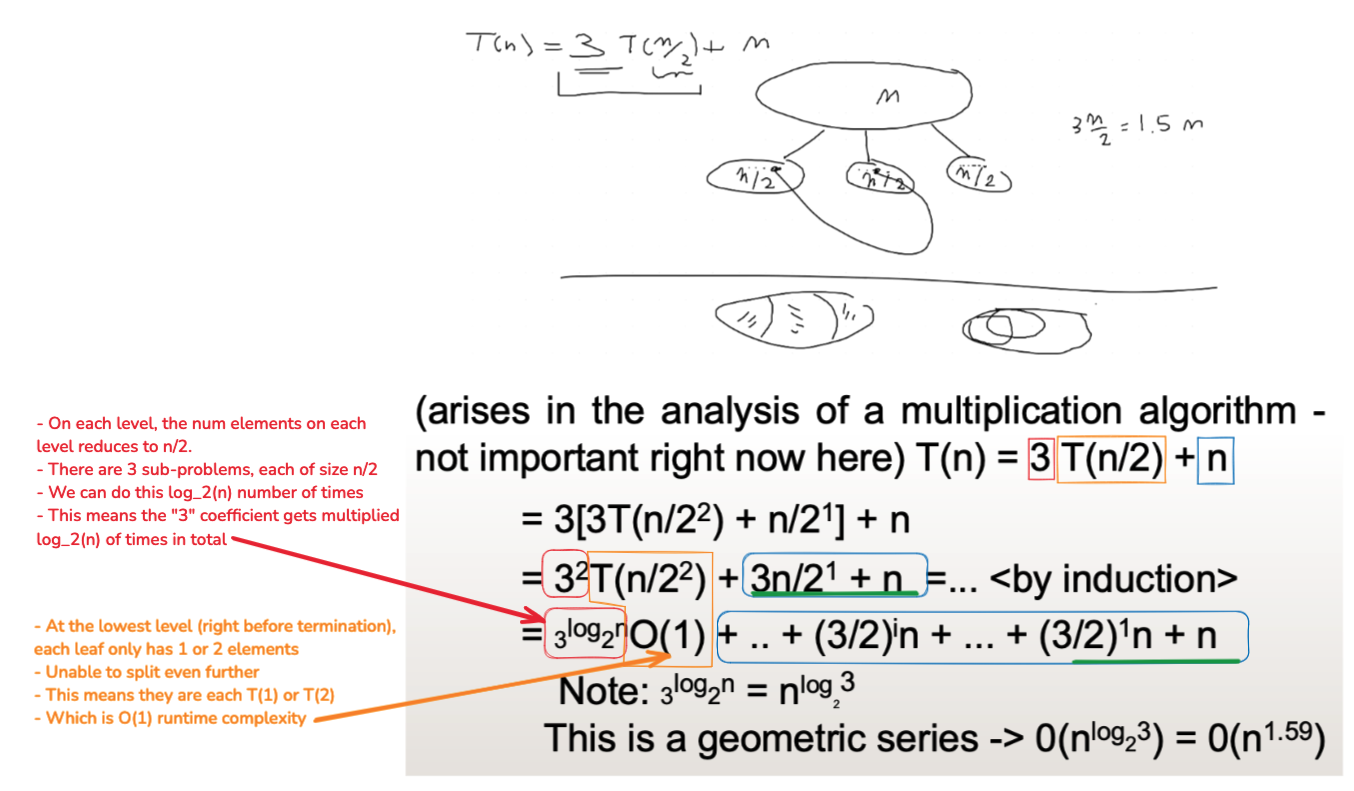
?. Recursion Tree

How does this work?