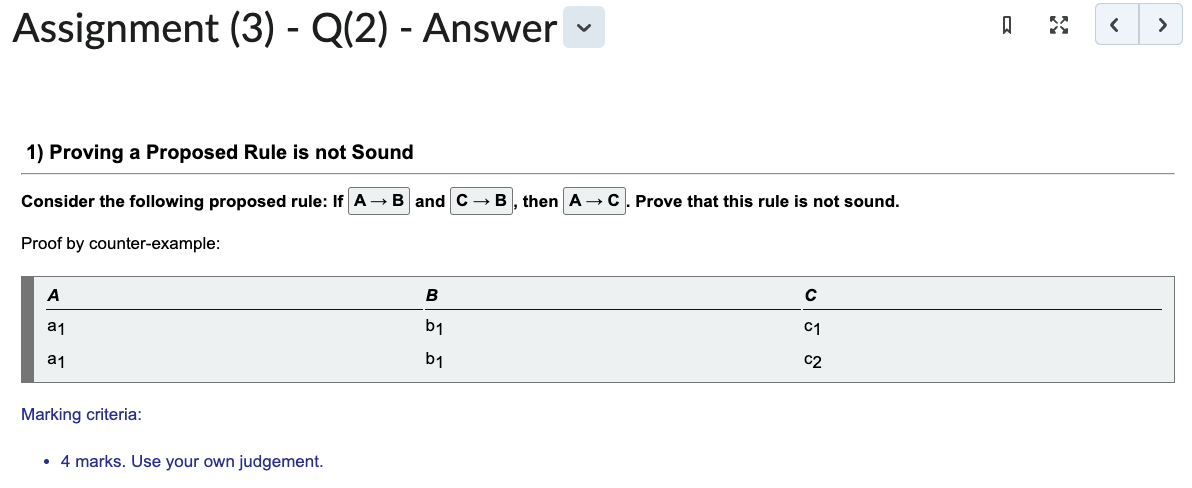
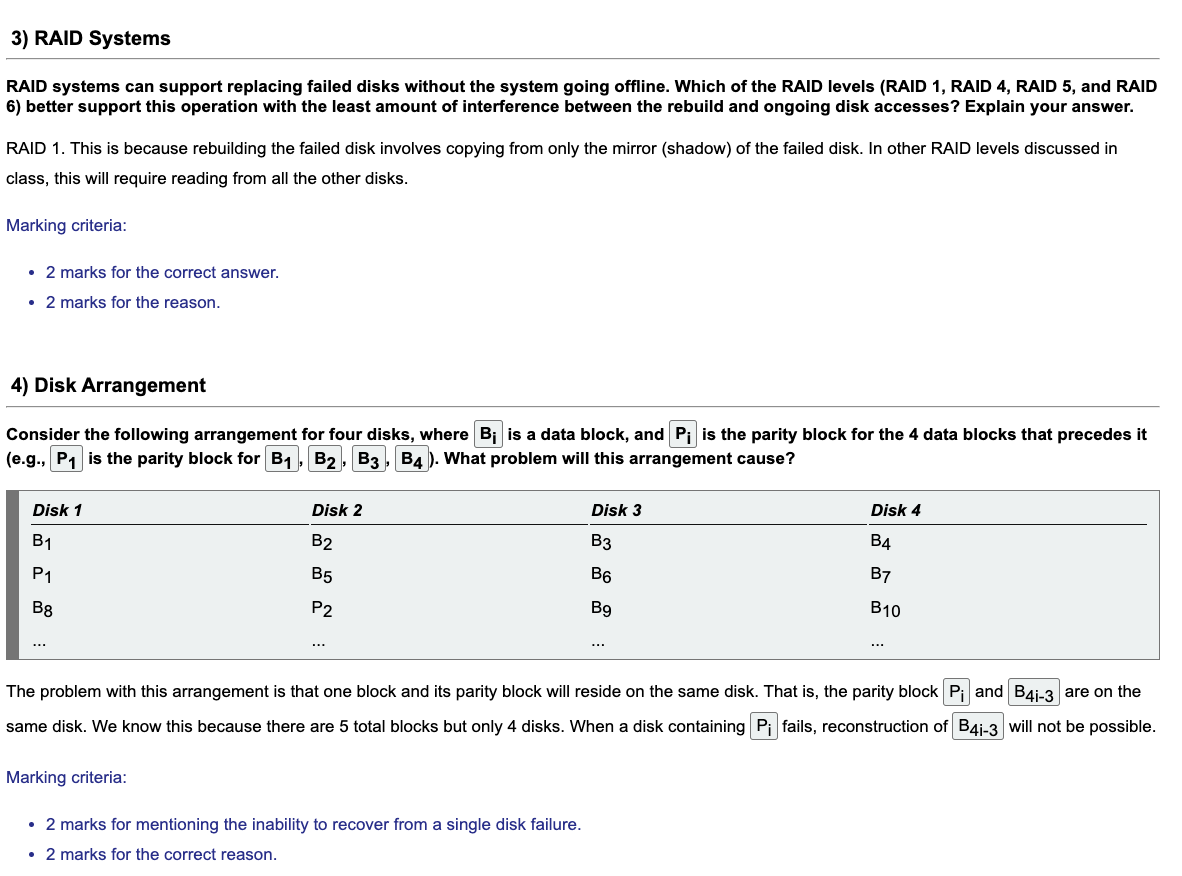
Normalization Theory

Functional Dependencies

Aside

• Quick way to remember: studentID (PK) $\rightarrow$ studentName.
• studentID determines studentName.

studentID	studentName	courseCode	valid?
stu001	Bob	COMP 3000	✅
stu002	Jane	COMP 3005	✅
stu003	Bob	COMP 1405	✅
stu003	Bob	COMP 1406	✅
stu001	James	COMP 2402	❌ Contradicts row 1. If this row exists, then studentID $\rightarrow$ studentName is false.

Trivial Functional Dependencies

• A functional dependency $X \rightarrow Y$ is trivial if $Y \subseteq X$.
• $XY \rightarrow Y$ is trivial.
• $Y \rightarrow XY$ is non-trivial.

Armstrong's Axioms

1. Reflexivity: If $XY \rightarrow X$, then $X \rightarrow Y$.
2. Augmentation: If $X \rightarrow Y$, then $XZ \rightarrow YZ$.
3. Transitivity: If $X \rightarrow Y$ and $Y \rightarrow Z$, then $X \rightarrow Z$.
4. Union: If $X \rightarrow Y$ and $X \rightarrow Z$, then $X \rightarrow YZ$.
5. Decomposition: If $X \rightarrow YZ$, then $X \rightarrow Y$ and $X \rightarrow Z$.
6. Pseudotransitivity: If $X \rightarrow Y$ and $WY \rightarrow Z$, then $WX \rightarrow Z$.

Superkeys and Candidate Keys

$R = (A, B, C, G, H, I) \\ (AG)^+ = ABCGHI$

• Superkey: All attributes in the relation are determined by this key. In this example, $AG$ is a superkey.
• Candidate Key: A small subset of attributes that each individually uniquely determine all other attributes in the relation. In this example, if $AG$ is a candidate key, it has to mean A and G can uniquely determine all other attributes in the relation (individually).

Assignment 3